【Acwing 周赛复盘】第86场周赛复盘(2023.1.14)
周赛复盘 ✍️
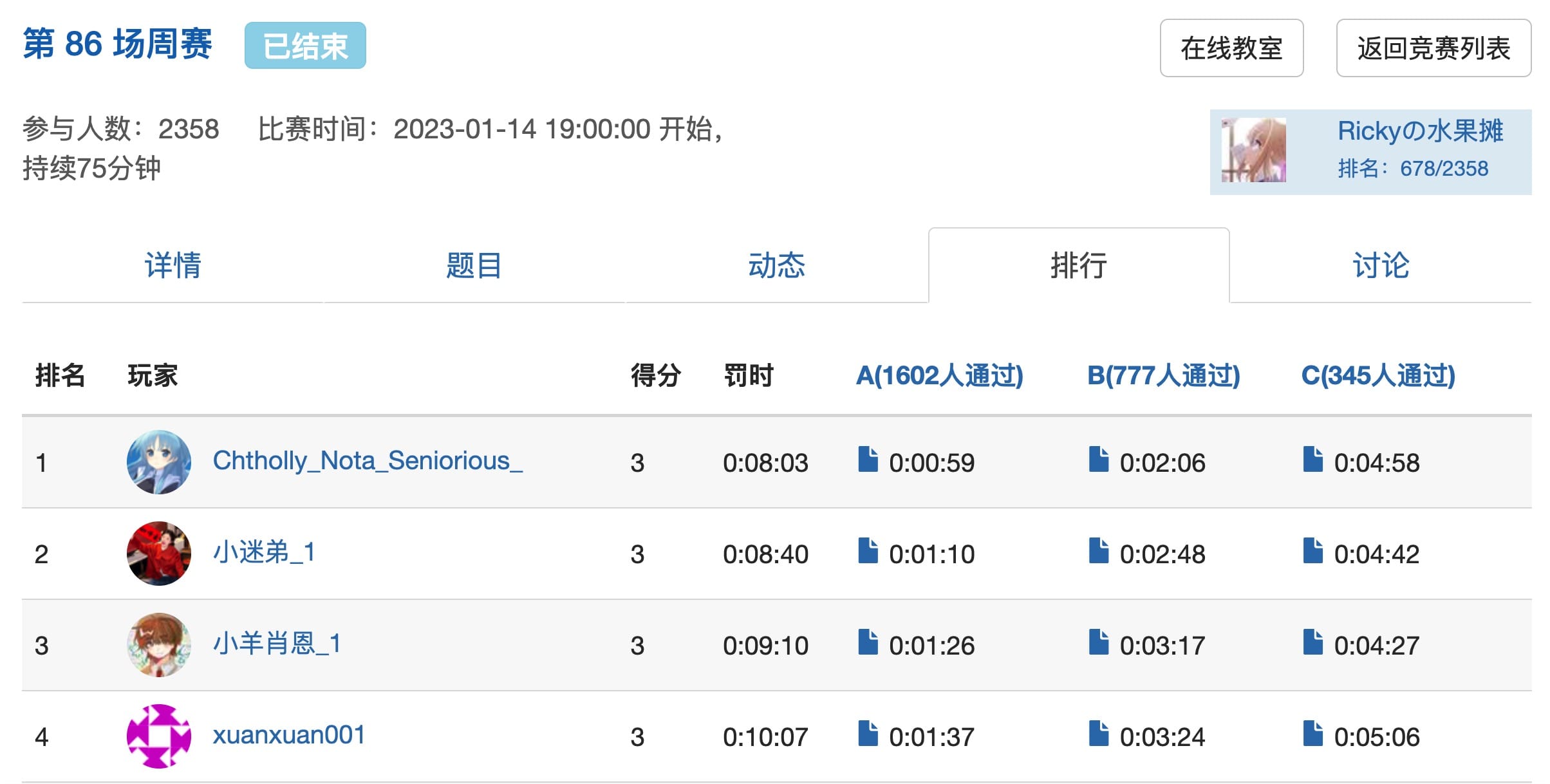
本周个人排名:678/2358(28.7%)
AC情况:2/3
这是博主参加的第一次周赛,深刻体会到了世界的参差 😂
看到排名 TOP3 的大佬都是不到 5 分钟内就 AK 了,真是恐怖如斯(ORZ)
对比下来,自己做满 75 分钟并且只 AC 了 2 题真是弱爆了。。。
希望未来也能继续努力,紧跟大佬们的步伐,继续加油 💪
周赛信息 📚
时间:2023年1月14日19:00-20:15
竞赛链接:https://www.acwing.com/activity/content/2794/
y总直播间:http://live.bilibili.com/21871779
y总录播讲解视频:【AcWing杯 - 第86场周赛讲解】
题目列表 🧑🏻💻
| 题目名称 | 原题链接 | 难度 |
|---|---|---|
| 4794. 健身 | 原题链接 | 简单 🟢 |
| 4795. 安全区域 | 原题链接 | 中等 🟡 |
| 4796. 删除序列 | 原题链接 | 困难 🔴 |
题解 🚀
【题目A】健身
【题目描述】
李华一共要进行 $n$ 组健身训练。
其中,第 $i$ 组训练的时长为 $a_i$。
李华只做三种运动:胸部(chest)运动、二头肌(biceps)运动、背部(back)运动。
而且,三种运动是循环训练的,也就是说他第一组训练是胸部运动,第二组训练是二头肌运动,第三组训练是背部运动,第四组训练是胸部运动,第五组训练是二头肌运动……以此类推直到做完第 $n$ 组训练。
请你计算,他做哪种运动的 时长 最长。
【输入】
第一行包含整数 $n$。
第二行包含 $n$ 个整数 $a_1,a_2,…,a_n$。
【输出】
共一行,如果训练时长最长的运动为:
- 胸部运动,则输出
chest。 - 二头肌运动,则输出
biceps。 - 背部运动,则输出
back。
数据保证训练时长最长的运动是唯一的。
【数据范围】
前 $3$ 个测试点满足 $1 \le n \le 7$。
所有测试点满足 $1 \le n \le 20$,$1 \le a_i \le 25$。
【输入样例1】
2
2 8【输出样例1】
biceps【输入样例2】
3
5 1 10【输出样例2】
back【输入样例3】
7
3 3 2 7 9 6 8【输出样例3】
chest【原题链接】
https://www.acwing.com/problem/content/4797/
【题目分析】
签到题,简单模拟即可。(但是现场编写的代码有很多可以改进和优化的地方,见下面「代码对比总结」部分)
【复盘后的优化代码】✅
#include<bits/stdc++.h>
using namespace std;
int s[3];
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
int n;
cin >> n;
int x;
for (int i = 1; i <= n; ++i) {
cin >> x;
// 下面的写法避免了多个if
s[i % 3] += x; // s[1]存储chest、s[2]存储biceps、s[0]存储back
}
// 找到最大值下标
int k = 0;
for (int i = 1; i <= 2; ++i) {
if (s[i] > s[k])
k = i;
}
// 输出结果
if (k == 1) cout << "chest" << endl;
else if (k == 2) cout << "biceps" << endl;
else cout << "back" << endl;
return 0;
}【周赛现场 AC 代码】
#include<bits/stdc++.h>
using namespace std;
int n, tmp;
int chest,biceps,back;
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> tmp;
if (i % 3 == 1) {
chest += tmp;
} else if (i % 3 == 2) {
biceps += tmp;
} else {
back += tmp;
}
}
// cout << chest << " " << biceps << " " << back << endl;
if (chest > biceps) {
if (chest > back) {
cout << "chest" << endl;
} else {
cout << "back" << endl;
}
} else {
if (biceps > back) {
cout << "biceps" << endl;
} else {
cout << "back" << endl;
}
}
return 0;
}【代码总结分析】
s[i%3] += x的思路值得借鉴,省去了多个if判断- 寻找最大值下标的方式值得借鉴,优化了直接比较的多 if 判断
【题目B】安全区域
【题目描述】
给定一个 $n×n$ 的方格棋盘和 $m$ 个国际象棋中的车。
对于一个方格,如果该方格满足以下两个条件中的至少一个,则该方格会被车攻击到:
- 该方格内有车。
- 至少有一个车与该方格位于同一行或同一列。
现在,我们要将 $m$ 个车逐个放入到棋盘中,其中第 $i$ 个车放到棋盘的第 $x_i$ 行第 $y_i$ 列的方格中。
车的编号从 $1$ 到 $m$,行/列的编号从 $1$ 到 $n$。
保证任意两个车不会放到同一个方格中。
对于 $1 \le i \le m$,请你计算,将前 $i$ 个车放入到棋盘中后,有多少个方格不会被车攻击到。
【输入】
第一行包含两个整数 $n,m$。
接下来 $m$ 行,其中第 $i$ 行包含两个整数 $x_i,y_i$,表示第 $i$ 个车放到棋盘的第 $x_i$ 行第 $y_i$ 列的方格中。
【输出】
共 1 行,其中第 $i$ 行输出将前 $i$ 个车放入到棋盘中后,不会被车攻击到的方格数量。
【数据范围】
前 $3$ 个测试点满足 $1 \le m \le 3$。
所有测试点满足 $1 \le n \le 10^5$,$1 \le m \le min(10^5,n^2)$,$1 \le x_i,y_i \le n$。
【输入样例1】
3 3
1 1
3 1
2 2【输出样例1】
4 2 0【输入样例2】
5 2
1 5
5 1【输出样例2】
16 9【输入样例3】
100000 1
300 400【输出样例3】
9999800001【原题链接】
https://www.acwing.com/problem/content/4798/
【题目分析】
思维题,需要通过 数学推导 的方式,得到未被攻击的方格数数量为:$(n-c)*(n-r)$,其中 $c,r$ 为被攻击的列数、行数
🍉 PS:本题数据范围较大,需要使用 long long 类型,不然会报错。(在公式前强制转换即可:(ll)(n-c)*(n-r))
【复盘后的优化代码】✅
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int n, m, x, y;
int a[N], b[N];
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
cin >> n >> m;
int row = 0, col = 0;
for (int i = 1; i <= m; ++i) {
cin >> x >> y;
// 统计当前被攻击的行数、列数
if (!a[x]) a[x] = 1, row++;
if (!b[y]) b[y] = 1, col++;
// 求剩余个数的公式,该形式容易推导和记忆
cout << (ll) (n - row) * (n - col) << " ";
}
return 0;
}【周赛现场 AC 代码】
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int n, m, x, y;
ll ans[N];
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
cin >> n >> m;
ll sum = (ll) n * n;
int row = 0, col = 0;
for (int i = 1; i <= m; ++i) {
cin >> x >> y;
if (!a[x]) a[x] = 1, row++;
if (!b[y]) b[y] = 1, col++;
cout << (ll) sum - (ll) row * n - (ll) col * (n - row) << " ";
}
return 0;
}【代码对比总结】
- 推导的公式,可以写成 $(n-c)*(n-r)$ 这样更加 简洁且容易记忆 的形式。
- 在使用
(ll)的 强制转换 时,需要注意 哪些项会爆 int。(本次周赛敲代码时,由于没有考虑该问题,以为在最前面加上(ll)就能整体转换,导致(ll) sum - row * n - col * (n - row)这样 爆int 的错误没能被及时发现,极大的影响了 AC 时间和心态)
【题目C】删除序列
【题目描述】
给定一个长度为 $n$ 的正整数序列 $a_1,a_2,…,a_n$。
你可以进行任意次删除操作。
每次删除操作分为两步:
- 选择序列中的 一个 元素(不妨设其元素值为 $x$),并将这 一个 元素删除,这可以给你加 $x$ 分。
- 将 所有 的 元素值 为 $x−1$ 和 $x+1$ 的元素(如果有的话)从序列中删除,这不会给你带来任何分数。
请计算,通过删除操作,你可以获得的最大得分。
【输入】
第一行包含整数 $n$。
第二行包含 $n$ 个正整数 $a_1,a_2,…,a_n$。
【输出】
一个整数,表示可以获得的最大得分。
【数据范围】
前 $6$ 个测试点满足 $1 \le n \le 10$。
所有测试点满足 $1 \le n \le 10^5$,$1 \le a_i \le 10^5$。
【输入样例1】
2
1 2【输出样例1】
2【输入样例2】
3
1 2 3【输出样例2】
4【输入样例3】
9
1 2 1 3 2 2 2 2 3【输出样例3】
10【原题链接】
https://www.acwing.com/problem/content/4799/
【题目分析】
动态规划题,需要平时积累,详细讲解见 y总讲解录像:链接
【二刷经历】
2023 年 4 月 8 日(考完蓝桥杯的晚上),摊主想要把这篇文章上传至自己的博客网站,于是再次阅读了这篇寒假写的复盘,打算检查文章可能存在的错误。
在检查的过程中,摊主突然发现 C 题又不会做了,说明当时还是没有理解透彻,需要回炉重造。😂
回顾一下自己晚上的做题流程:
- 一开始打算用贪心去解,即优先删去最大值,但是样例3这样的序列显然无法这样简单的贪心。
- 然后发现可以把无序的序列,进行升序排列,更加直观。
- 想到使用 线性DP 求解,但是始终无法推出状态转移方程,或者说究竟如何表示状态?
- 自己模拟的序列是这样的
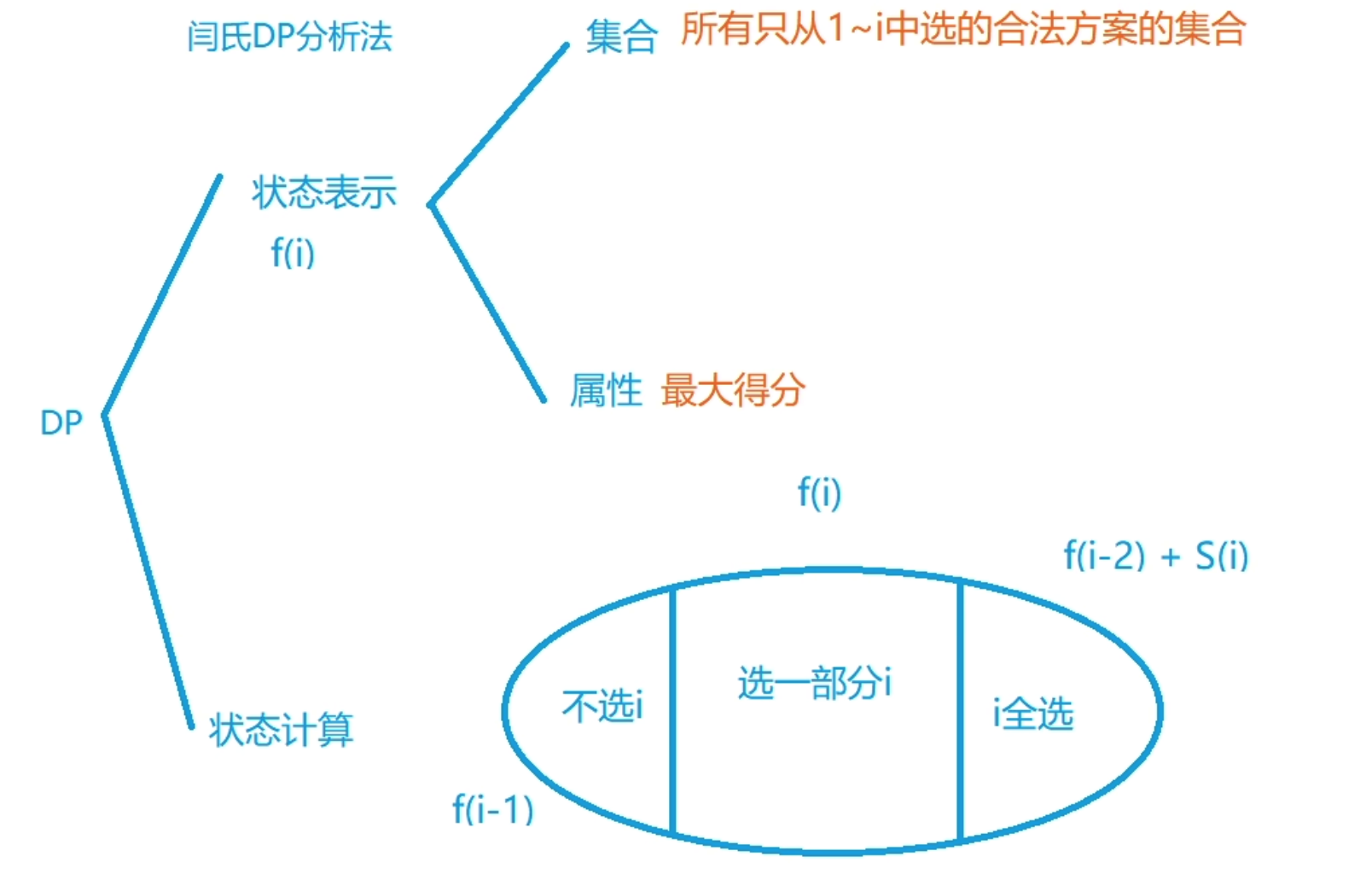
1 1 1 2 2 2 2 2 3 3 3 - DP 考虑如下
dp[i]表示删去第i个数字后(一定要删去第i个数字),能得到的最大值dp[i]表示1~i序列能得到的最大值(不一定删去第i个数字)
- 但是在考虑上面两种情况是,总是会遇到 无法往下思考的点(这种状态在题目难时经常出现),有时候情况有点杂,自己就开始理不清了。
- 比如第 1 种情况,如果一定删去第
i个数字a[i],那这时候如何删除前面所有的a[i]-1?状态好像没办法转移过来,或者说需要记录一连串数字的左右下标,感觉有点麻烦。(其实这里就应当考虑到,如果把一连串数字进行合并,会不会简单些) - 再如第 2 种情况,那就需要讨论是否删除第
i个数字,但是这样也需要讨论:比如1 1 1 2,执行到 2 时,如果删了 2,dp[4] = 2,不删 2 的话,dp[4] = 3,取两者最大值 →dp[4] = 3。但是假如在后面再添一个2,我们一眼能看出来dp[5] = 4,但是落实到具体方程时,dp[5]=dp[4]+2=5,显然有问题,因为这时候dp[4]应该为 2,出现了前后矛盾。
- 比如第 1 种情况,如果一定删去第
- 自己模拟的序列是这样的
- 最后只能遗憾告终
于是又去温习了一遍 y总的讲解,发现一开始 y总直接把 1 1 1 2 2 2 2 2 3 3 3 这种合并成了 1 2 3,就直接对 3 个数值进行 线性DP,省去了记录一连串数字的左右下标。(这里有一步贪心过程,如想要删除数字 2,一定是把 5 个 2 都删除)
然后 dp[i] 的表示是选择了上面线性DP的第二种方案,思路如下:
- 序列
1 2 ... i,这里i并非下标,而是原序列中出现的值- 如果不选数字
i,则dp[i] = dp[i-1] - 如果选择数字
i,则dp[i] = dp[i-2] + s[i] - 取两者最大值即可。
- 注意 🍉:由于状态转移方程中出现了
i-2,所以为了防止下标越界,循环需要从 2 开始;或者写成这种形式dp[max(0,i-2)]
- 如果不选数字
这里非常精妙的对数值进行线性DP,而不是像很多模型那样对下标进行线性DP(有点像「二分答案」那样)
只能说 DP 的题目思路都太精妙了,只有多看,多学,多练,才能让自己「顿悟」,继续加油。
【复盘后的优化代码】✅
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
ll s[N], dp[N];
int n, x;
int main() {
ios::sync_with_stdio(false); //cin读入优化
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> x;
s[x] += x; // s数组类似于"桶",这里的"桶"直接存储总和
}
// 动态规划
for (int i = 1; i <= N - 1; ++i) {
// 状态转移方程
dp[i] = max(dp[i - 1], dp[max(0, i - 2)] + s[i]);
}
cout << dp[N - 1] << endl;
return 0;
}【周赛现场 AC 代码】
该题现场未AC 😂
【代码对比总结】
- 周赛现场没能看出本题为动态规划题,导致蛮力模拟一直解不出来。说明需要 多做题,多积累。
🍉 PS:推荐前往摊主的个人博客查看该文章,可以有更好的阅读体验



